Improving the way neural networks learn(weight initialization)

Posted on | In

说在前面的话：这是Improving the way neural networks learn系列的完结篇，标题虽有’weight initialization’的注释，但内容远远不止这一方面，甚至有点杂。

Weight initialization

之前的所有代码中，weight和bias初始化为两个均值为0、标准差为1的独立高斯随机变量

1
2
3
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)
                for x, y in zip(self.sizes[:-1], self.sizes[1:])]

不妨假设input层有1000个神经元，假设一半的input是1，另一半是0，由公式
$$
z=\sum_jw_jx_j+b
$$
由于高斯随机变量线性组合之后仍是高斯随机变量，显然z为501个高斯随机变量之和，均值仍为0，方差则是(501)1/2≈22.4（这边关于高斯分布的相关概率论知识没有学到，正自学中，所以不甚了解），画出z的概率密度函数曲线：

z

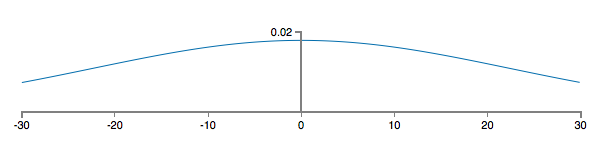
发现z的取值绝对值很有可能非常大，这样代入到sigmoid函数后，就会出现neuron饱和，即学习率较低的问题，之前提到用cross-entropy cost function解决这一问题，作者也提到:

We addressed that earlier problem with a clever choice of cost function. Unfortunately, while that helped with saturated output neurons, it does nothing at all for the problem with saturated hidden neurons.

这段话我开始不太明白，什么叫只能帮助解决输出层neurons饱和问题，明明cost function对每一层的weights都求导了啊，但这似乎可以这样理解：单独考虑网络中间的hidden layers（不考虑output layer），即暂时“舍弃”cost function，以中间某层的activation对之前的weight求导，显然会出现饱和的情况。而加入互熵损失，这些饱和就被“约掉”，即表面上看不出中间层饱和问题（这仅仅是我的理解）。
直观来说，需要减小方差使得概率密度曲线的幅度不那么大，作者因此将weight初始化为均值为0、标准差为1/(nin)1/2的高斯变量，bias的初始化不变（bias的影响相对较小）:

1
2
self.weights = [np.random.randn(y, x)/np.sqrt(x)
                for x, y in zip(self.sizes[:-1], self.sizes[1:])]

经计算可发现输出z的均值为0，标准差为(500/1000+1)1/2=(3/2)1/2=1.22……概率密度曲线如下：

z

这就解决了上面的问题，训练得到如下结果：

train

How to choose hyper-parameters

在神经网络中不可避免地会遇到超参数的选择问题，这势必需要许多次的实验，所以前期的目标并不是提升网络的性能，而是快速得到实验反馈，为此，可以减少数据的类别（如仅取‘0’、‘1’两类图片）、简化网络（去掉hidden layer）、减少数据集的规模等等——这是我们选取参数的board strategy。
除了人工调参，目前还有自动化优化参数工具，如grid search等。

Learning rate

显然，过大的learning rate会导致训练时越过cost function的“valley”，反而导致cost上升；过小的learning rate会导致学习过慢。对于前者，有更准确的解释：梯度下降使用了cost function的一阶近似，但随着η的增大，Talyor展开的高阶项将变得难以忽略。选取η策略便是找到其“阈值”，通俗来说就是仍能使cost下降且使得“步长”尽量大的η。如果前几个周期cost在decrease，就试着增大η直至cost开始上升；反之同理。一般来说η的取值都不应超过“阈值”（废话），在识别手写数字任务中η取值为0.5。
另外，η还可以采用“先大后小”的取值策略，以便更精确地到达”valley”。具体说，先采用固定的η，但当validation accuracy开始下降时，将η减半，如此反复，知道η变成初始值的1/1024停止。

Training epochs

这里的方法就是之前说过的early stopping，代码也展示过了。即如果accuracy在n训练周期没有increase的话，就停止训练，这种策略也称no-improvement-in-n epochs strategy。但这有一个问题，某些情况下accuracy会有一个“高原期”，过了这段时间之后仍会上升，这就又带来了参数n的选取问题。

Regularization parameter

这个没有多少trick，就是普通的取值、训练、比较。

Mini-batch size

这部分内容有点烦人，我并未完全理解，可直接跳过去看调参方法。我疑惑点在于：
①作者最后对于参数过大和过小的缺陷的解释似乎是建立在使用online learning+matrix update的基础上的，但代码中用的是循环策略。
②作者反复强调online learning的好，即可以快速更新权重，但这和较大的mini-batch size可提升学习速度关系何在？
③最后举η扩大100倍，但时间只扩大了了约50倍的例子作用是什么。
首先抛出下面一大堆分析的结论：使用较大的mini-batch会提高学习速度。需要注意的是，这里的速度提高并不是epoch减少，而仅仅是程序优化后学习时间的减少（更充分发挥了硬件的性能）。
首先，对于我们的任务online learning是可行的，即mini-batch的大小为1，每训练完一个input后就直接更新权重。online learning的可能问题在于，单一的训练数据可能会导致weight向错误的方向更新，但分析后发现这并无影响。因为我们并不需要每个input都使权重准确地更新，即某个input导致的错误更新并不会导致最后结果的变化——cost function总是会到达“valley“的。
好了，接下来扩大mini-batch，不妨设其size为100，仍使用online learning，即此时把整个mini-batch当作一个input直接更新weight和bias，使用矩阵方法（作者在之前的chapter指出过，就是把每个input写成列向量，再全部组合成一个matrix，以矩阵形式更行权重），可以对mini-batch里的所有数据一次性更新梯度:
$$
w→w-\eta\nabla C_x
$$
而不是之前（代码中已经添加了正则项）遍历每一个input最后再update：
$$
w→w-\eta\frac{1}{100}\sum_x\nabla C_x
$$

1
2
3
4
5
6
7
8
for x, y in mini_batch:
    delta_nabla_b, delta_nabla_w = self.backprop(x, y)
    nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
    nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw
                for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
                for b, nb in zip(self.biases, nabla_b)]

由于矩阵的运用使得前者花费的时间只有后者的一半左右。不妨把学习率η扩大100倍，则使用循环策略的权重更新公式为
$$
w→w-\eta\sum_x\nabla C_x
$$
看上去这像是进行了100次online learning，但实际上画的时间大概只有单一的online learning的50倍（虽然理论上的时间也并不是单一online learning的100倍，因为weight变化了，但肯定大于50倍），然后得出结论:

It seems distinctly possible that using the larger mini-batch would speed things up.

但mini-batch size也不能过大，否则weight得不到足够多的更新；过小则不能充分发挥矩阵运算库的优势（这似乎表明作者的分析都是建立在使用online learning的基础上）。（这一句才是重点，前面的分析感觉作者自己都没说清楚，非常乱），所以要折中考虑。幸好其他参数与mini-batch size关联不大，即我们并不需要先优化好其他参数才能找到最好的mini-batch size，所以只要画出不同mini-batch size下的accuracy-time图像，选择最快的那个参数就行了。

以上就是调参的全部内容，但仍有一个问题，用作者话来说就是：
In practice,there are relationships between the hyper-parameters.

Other techniques

这里介绍了SGD以外的两种训练方法。

Hessian technique

目标仍是最小化cost function，它可以看作w的函数，即C=C(w)，其中w=w1,w2……在w点处Talyor展开：

展开

写成矩阵形式：
$$
C(w+\Delta w)=C(w)+\nabla C\cdot\Delta w+\frac{1}{2}\Delta w^TH\Delta w+……
$$
H就i是Hessian matrix。忽略掉高阶项，有
$$
C(w+\Delta w)≈C(w)+\nabla C\cdot\Delta w+\frac{1}{2}\Delta w^TH\Delta w
$$
想得到变换后C的最小值，于是右边对Δw求导，极小值在
$$
\Delta w=-H^{-1}\nabla C
$$
取到（前提是H为正定矩阵，否则就是极大值）。
于是Hessian方法的一般步骤为：

1.初始化w
2.根据公式
$$
w’=w-H^{-1}\nabla C
$$
更新weights。
3.更新w’:
$$
w’’=w’-H^{‘-1}\nabla’C
$$
在实际操作中，Δw之前也需要乘learning rate，即
$$
\Delta w=-\eta H^{-1}\nabla C
$$
然而，一旦input weights过多，Hessian矩阵的计算量也就变得十分庞大，因此这种方法局限性较大。

Momentum-based gradient descent

前面Hessian technique因为保留了二阶项，所以它不仅保留了梯度，还结合了梯度的变化趋势（H term），基于momentum的梯度下降技术也有这样的优点。
该方法引入了速度(v)，摩擦力(μ)参数，原本的梯度下降规则
$$
w→w’=w-\eta\nabla C
$$
改为
$$
v→v’=\mu v-\eta\nabla C
$$

$$
w→w’=w+v’
$$

速度v可以理解为梯度的变化速度（虽然很不恰当），μ则是用来控制速度的。当μ=1是，w中的v项会累积得越来越大（这个可以轻松证明），所以cost也会下降得越来越快，但显然这样会出现overshoot的情况；另一个极限是μ=0，即friction很大，此时v无法累计，w的更新与普通的梯度下降无异。所以，选择一个恰当的μ值，既可以使velocity累积，保证学习速度，又可以防止overshoot。

Other models of artificial neurons

这里介绍了tanh和rectified linear unit，前者其实就是sigmoid的变形
$$
tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}
$$

$$
\sigma(x)=\frac{1}{1+e^{-z}}=\frac{1+tanh(z/2)}{2}
$$

函数图象和sigmoid类似，只不过值域变成了(-1,1)，由公式
$$
\frac{\partial{C}}{\partial{w^l_{jk}}}=a^{l-1}_k\delta^l_j
$$
若用sigmoid函数，a恒正，若δlj为正，则l层第j个neuron与(l-1)层相联的所有weights都会减小；反之都会增大。即此时两层之间的权重的变化只与后层的error有关，而与前层无关。于是此时值域为(-1,1)的tanh neuron的好就显现出来了，但它同样面领着输入过大时neuron饱和的问题。

后者即为ReLU，它会过滤掉那些负输入（容易看出负输入不会导致更新），另外也不会有输入过大导致的饱和问题，所以其应用比sigmoid和tanh都广泛，性能当然更好。

Conclusion

神经网络涉及到许多参数、超参数，所以要想完全清楚其运行过程细节仍然十分困难。另外，之前许多解释、证明都是经验性的，怎么说呢，有好也有坏吧。

0%